最小二乗法
$N$個のデータ$(x_1,y_1),\cdots,(x_N,y_N)$に対してある直線をあてはたい。
各データを近似できる直線を以下のように定義する。
$
y = ax+b
$
この直線の $a$ と $b$ を求めたい。
点 $(x_n,y_n)$における、近似された直線の$y$軸の値$y’_n$の値は
$
y’_{n} = ax_n + b
$
であるから、実際の点と近似された点との誤差 $t$は
$
t = y’_{n} – ( ax_n + b )
$
と表すことができる。
$t$ はプラスとマイナスの誤差で打ち消されていまうので
この2乗和を考え、各点の誤差の合計を最も小さくする変数 $a,b$ を求められれば良い。
$$
J = \sum_{n=1}^{N}( y’_{n} – ( ax_n + b ) )^2 \tag{1.2}
$$
式(1.2)を最小化する $a,b$ を求める。
式(1.2) をそれぞれ$a$ , $b$ で偏微分で得られた導関数が0となる解を求めれば良い。
$$
\frac{\partial J}{\partial a} = 0 , \frac{\partial J}{\partial b} = 0 ,
$$
具体的に偏微分してみると
$$
\tag{1.3} \frac{\partial J}{\partial a} = a\sum_{n=1}^{N}x_n^2 + b\sum_{n=1}^{N}x_n – \sum_{n=1}^{N}x_ny_n
$$
$$
\tag{1.4} \frac{\partial J}{\partial b} = a\sum_{n=1}^{N}x_n + b\sum_{n=1}^{N}1 – \sum_{n=1}^{N}y_n
$$
解法1
式(1.3)(1.4)は、これは連立1次方程式の形であり、これを解いて$a,b$を求めればよい。
Numpyの連立1次方程式を解く関数を使う
import numpy as np
random y = np.array([ 3 * x + 5.0 +random.random()*6 for x in range(10)]) x = np.arange(10)
%matplotlib inline
from matplotlib import pyplot as plt
plt.scatter( [x for x in range (10)], y)
<matplotlib.collections.PathCollection at 0x1163635c0>

sum_XX = np.sum(x**2)
sum_X = np.sum(x)
sum_1 = 10
sum_XY = np.sum( x * y)
sum_Y = np.sum(y)X= np.array([[sum_XX,sum_X],[sum_X,sum_1]])
Y = np.array([sum_XY,sum_Y])
a,b = np.linalg.solve(X,Y)
print(a)
print(b)3.011018356776419
7.4796487811962065
%matplotlib inline
from matplotlib import pyplot as plt
plt.scatter( [x for x in range (10)], y)
plt.plot( [x for x in range(10)],[ x*a + b for x in range(10)],c='r')
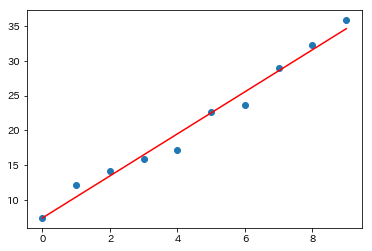
Scikit-learnのLenearRegressionを使う
from sklearn import linear_model
clf = linear_model.LinearRegression()
train_x = x.reshape(10,1)
train_y = y.reshape(10,1)
c = clf.fit(train_x,train_y)
a = clf.coef_[0][0]
b = clf.intercept_[0]
print (f'a={a},b={b}')
a=3.07969308080669,b=7.640591467908642
Tensorflow を使い 勾配降下法で解く
import tensorflow as tf
x1 = tf.placeholder(tf.float32, [None, 2])
w = tf.Variable(tf.zeros([2, 1]))
y1 = tf.matmul(x1, w)
t = tf.placeholder(tf.float32, [None, 1])
loss = tf.reduce_sum(tf.square(y1 - t))
train_step = tf.train.AdamOptimizer().minimize(loss)
sess = tf.Session()
sess.run(tf.initialize_all_variables())
train_t = np.array(y);
train_t = train_t.reshape([10, 1])
train_x = np.array([ [ 1, i] for i in range(10)],dtype='float32')
i = 0
for _ in range(100000):
i += 1
sess.run(train_step, feed_dict={x1:train_x, t:train_t})
if i % 10000 == 0:
loss_val = sess.run(loss, feed_dict={x1:train_x, t:train_t})
print ('Step: %d, Loss: %f' % (i, loss_val))
w_val = sess.run(w)
print (w_val)
def predict(x):
result = 0.0
for n in range(0, 2):
result += w_val[n][0] * x**n
return result
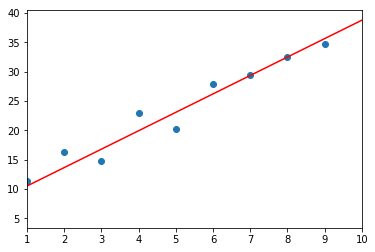
fig = plt.figure()
subplot = fig.add_subplot(1, 1, 1)
subplot.set_xlim(1, 10)
subplot.scatter(range(10), train_t)
linex = np.linspace(1, 10, 100)
liney = predict(linex)
subplot.plot(linex, liney,c='r')
plt.show()
WARNING:tensorflow:From <ipython-input-42-15b73738fe80>:11: initialize_all_variables (from tensorflow.python.ops.variables) is deprecated and will be removed after 2017-03-02.
Instructions for updating:
Use `tf.global_variables_initializer` instead.
Step: 10000, Loss: 44.583672
Step: 20000, Loss: 36.941315
Step: 30000, Loss: 36.941315
Step: 40000, Loss: 36.941307
Step: 50000, Loss: 36.941315
Step: 60000, Loss: 36.941319
Step: 70000, Loss: 36.941307
Step: 80000, Loss: 36.941338
Step: 90000, Loss: 36.941315
Step: 100000, Loss: 36.941322
[[7.3787937]
[3.138206 ]]